数学物理方法复习笔记之复变函数

第一章 解析函数

1. 复数的基本性质

1.1 复数及其运算

虽然这一节其实没啥好说的但是出于兴趣我还是找了个自己很满意的数学定义。

一个复数是一个有序实数对，其中。
复数的集合记作，即。
在此基础上，我们定义复数的相等、加法和乘法运算：

1. 相等 (Equality): 两个复数和相等，当且仅当它们的对应分量相等：

2. 加法 (Addition): 两个复数和的和定义为：

3. 乘法 (Multiplication): 两个复数和的积定义为：

因此，我们就有了复数的域结构 (Field Structure): 集合连同上述定义的加法和乘法运算，构成一个域 (Field)。这意味着它满足所有域的公理，包括加法和乘法的结合律、交换律、分配律，存在加法和乘法单位元，以及除零以外所有元素的加法和乘法逆元。

定义虚数单位 (Imaginary Unit): 我们定义虚数单位为复数。根据乘法定义，我们可以计算

由于被识别为实数，因此我们得到标志性的关系：

1.2 复数的表示

1.2.1 复平面

A.笛卡尔坐标形式 (Cartesian Form / Rectangular Form)

表示:
元素:

1. : 实部 (Real Part) ，记作。
2. : 虚部 (Imaginary Part) ，记作。
3. : 虚数单位，满足。
4. 几何意义: 复平面上的点。
5. 横轴（X轴）是 实轴 (Real Axis) 。
6. 纵轴（Y轴）是 虚轴 (Imaginary Axis) 。

B.极坐标形式 (Polar Form / Trigonometric Form)

表示:，结合欧拉公式 (Euler’s Formula) 写作

元素:

1. : 模 (Modulus / Magnitude / Absolute Value) ，记作计算公式：。几何意义为复平面上点到原点的距离。
2. : 辐角 (Argument) ，记作。计算公式：(需注意象限)。几何意义为：从正实轴逆时针旋转到向量的角度。

主辐角 (Principal Argument) ：记作（大写A），是辐角的一个特定取值，限制在区间或，最常见的是。对于给定的，主辐角是唯一的。

辐角 (General Argument) ：记作（小写a）。是主辐角加上的所有可能值，即，其中（整数）。 对于给定的，辐角是多值的。

C.复共轭 (Complex Conjugate)

1. 表示: 如果，则其共轭复数记作或。
   • 笛卡尔形式：。
   • 极坐标形式：如果，则。
2. 几何意义: 复平面上点关于实轴的反射点。

1.2.2 球面表示 (Spherical Representation / Riemann Sphere)

1. 概念: 黎曼球面 (Riemann Sphere) 提供了一种将整个复平面（包括无限远点）映射到一个球面上的方法。
2. 方法: 球极投影 (Stereographic Projection) 。
   1. 想象一个单位球体，它的南极点接触复平面的原点。
   2. 球体的北极点作为投影中心。
   3. 对于复平面上的任意一点，画一条从北极穿过的直线。这条直线与球面相交的唯一另一点就是在球面上的投影。
3. 几何意义: 将一个二维平面上的点映射到一个三维球面的点，允许我们以一种几何上直观的方式处理复数的“无限大”概念。

1.3 复平面上的曲线与复方程

两大问题：

1. 已知复平面上曲线的方程，如何写出的复方程
2. 已知复方程或不等式，如何确定它们表示的图形
   其实没啥说的。注意到的原始定义本来是有序实数对就会发现它其实很像一个二维矢量，拿这个来看就行了。

2. 复变函数的基本性质

2.1 复变函数定义

设集合,若存在映射使得

则称或为的复变函数，也称为原象的象，记作，为自变量，为定义域。
因此有：
单叶函数 ：
多叶函数 ：

2.2 区域

定义区域 ：复平面内同时满足开集性和连通性的点集
概念太多，这里大概列一下，都是望文就能生义：
邻域、去心邻域、外点、内点、界点、边界、闭包（闭区域）

区域在左手边的方向叫边界正向

2.3 极限与连续

和实变函数一样

3. 复变函数的导数与微分

3.1 导数与微分

3.1.1 导数的定义

设函数在点的某个邻域内有定义。如果极限

存在，则称函数在点可导，并将此极限值称为在的导数，记作或

3.1.2 微分的定义

若是可微的，有

3.1.3 可微（可导）的条件

必要条件 ：如果复变函数在点可导（可微），那么和在处的偏导数都存在，并且满足 Cauchy-Riemann (柯西-黎曼) 方程 ：

简单记忆 ：实实=虚虚，实虚=-虚实

充要条件只是多了一条和在可导（可微）

3.2 导数的几何意义

实数函数中导数表示函数曲线在点处的切线斜率，某种意义上，它衡量了当发生一个微小变化时，相应变化的“拉伸”或“压缩”比例。
回到复变函数上.
首先需要理解，复变函数本质上定义了一个从平面到平面的映射 (一个实数对映射到另一个实数对)。
其次，复数乘法的几何意义就是旋转和缩放 （可以从极坐标表示清晰地看到）。
最后，回忆

会发现如果这样看那么

相当于一个变换矩阵

3.3 解析函数

3.3.1 解析函数及其定义

1. 若复变函数在及其邻域可导，则称在解析
2. 若复变函数在区域处处可导，则称在解析，为内的解析函数
3. 若在不解析，则称其为奇点

还有一个无穷远处解析的判定，但是比较容易就懒得写了

解析函数的和、差、积、商、复合、反函数都解析

3.3.2 解析的条件及推论

解析的充要条件就是上面说的可微的。这里主要说几个小推论：

1. 解析函数的实、虚部都是调和函数（）
2. 解析函数的实、虚部梯度向量正交（）（也就是等高线正交）
3. 无穷远解析则无穷远导数为0

3.3.3 初等解析函数

没什么好说的，幂函数、指数函数、三角函数、双曲函数这些，和实函数大差不差。
唯一需要提出来的是根式函数 ，它有新定义：

通过极坐标表达可以注意到它的多值性与周期，这个还挺重要的，引出了支点和单值分支的概念。可以看出对数函数也必然具有多值性

第二章 解析函数积分

嘻嘻嘻大芬来喽

1. 复变函数积分

1.1 围线及其方向

简单曲线（分段光滑无自交叉），简单围线（单连通区域的边界），复围线（复连通区域的边界）没啥好说的，就是个定义。
设函数在区域内连续，是内一条起点为、终点为的有向光滑（或分段光滑）曲线。

1.2 积分的定义

积分的定义过程如下：

1. 分割 : 将曲线依次分割成个小弧段，分点为。

2. 取样: 在每个小弧段上，任意选取一点。

3. 求和: 构造和式（黎曼和）：
   

4. 取极限: 当分割无限加密，使得最长的小弧段长度趋于零时（即），如果上述和式的极限存在且唯一（与分点和样本点的取法无关），则该极限值就是沿曲线的积分。

最终定义为：

1.3 积分公式

直接把代成和然后把代成和即可（其实是懒得写了）。
和曲线积分很像，复变函数积分通常与路径有关。
直接计算复变函数积分的时候，一般用圆+指数形式作为突破口。

小例子

可以自己动手算算。
积分的性质和实变没啥区别

2. 柯西积分

2.1 柯西积分定理

2.1.1 单连通

单连通柯西积分定理 ：设在单连通区域内解析，为内分段光滑的闭合围线，则有

推论 ：单连通区域内解析函数积分值路径无关

2.1.2 原函数

感觉没啥用，和实变函数差不多而且没法把微积分基本定理拓展过来，只能有一个解析函数的原函数单值解析的结论。

2.1.3 复连通

设是开区域，为在上的全纯函数。 若是由有限条分段光滑曲线组成的闭链（闭路径），且及其内部（即所围成的区域）都包含于中，则有

看下面给的图应该就懂了。更多的“洞”同理，只是相当于多加几个曲线积分。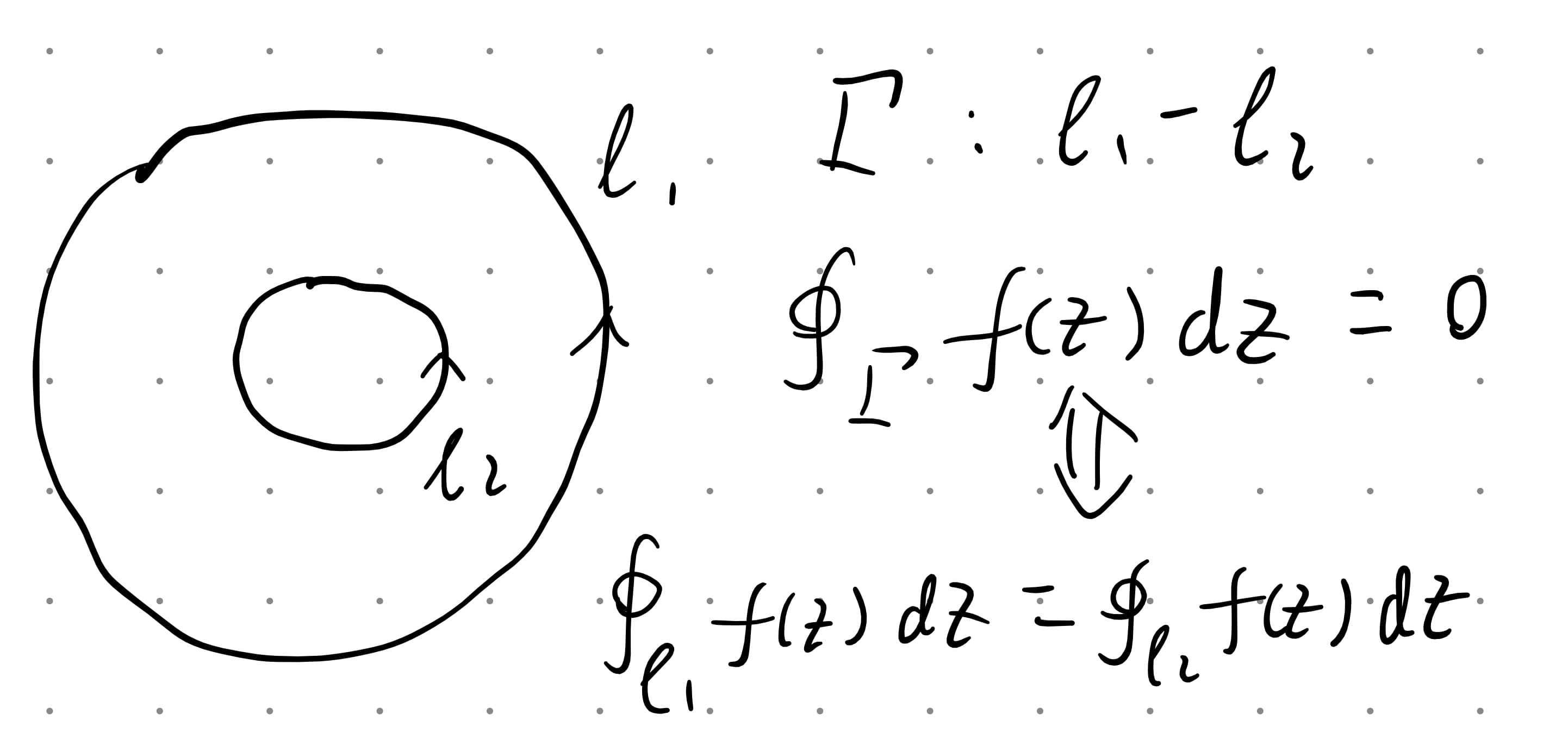

2.2 柯西公式

2.2.1 柯西积分公式

设为的边界围线，在内解析，在上连续，为任意内点，则

实际上一般我们是逆着（从右向左）用的。如果是复连通那就“多加几条线”。

2.2.2 导数形式的柯西积分公式

也很显然的一个公式，相当于对上面的式子求导而已。

小推论：开区域解析则无穷阶可导且导数均在区域解析。

小例题，可以动手算算

2.2.3 公式运用

解析函数几个小性质，平均值定理（感觉是凑数的），最大模原理（边界取最大），柯西不等式（不知道意义在哪），刘维尔定理（全平面解析、无穷远有界则为常数），代数学基本定理（刘维尔定理的推论），反正都没啥用感觉。毕竟我是学物理的。
有一个逆定理还有点意思：
莫雷拉定理 ：函数f(z)在单连通区域内连续，若对其中任意围线都有则在内解析。有一说一感觉也不是很有用。

第三章 无穷级数

老实说这一章开始我就没咋听课了

1. 复级数

虽然跟高数没什么区别但是我感觉高数级数部分快忘光了，所以还是复习一下。

1.1 复数项级数

1.1.1 收敛与发散的定义

太长了真不想写（无法想象会有人记这种），反正大概意思就是n趋于无穷和式极限存在就是收敛，否则发散。
还有一个绝对收敛的概念指的是级数所有项取绝对值时候的收敛情况

1.1.2 敛散性判据

柯西收敛判据

比较审敛法

绝对值大的如果都收敛，那另一个一定绝对收敛

比值审敛法

绝对收敛

根式判别法

绝对收敛

高斯判别法

绝对收敛

其实还有个M判别法，但我感觉没啥用这个

1.2 幂级数

定义

称为以b为中心的幂函数

1.2.1 收敛性

阿贝尔定理 ：若幂级数在收敛，则在内一致收敛

1.2.2 收敛半径

由阿贝尔定理，收敛域一定是圆，半径就叫收敛半径。

比值判别法

根式判别法

1.2.3 收敛幂级数的分析性质

大概就是说收敛圆内绝对一致收敛。

2. 泰勒级数和泰勒展开

2.1 泰勒展开本体

没啥说的和实函数一模一样，但是这里给出几个常用的泰勒展开式子，最好记住。
重中之重 指数函数泰勒展开：

没啥说的，既好记又好用
它变形（欧拉公式）能得到正余弦展开


重中之重 几何级数

记住适用条件（收敛域）
对它求积分就能得到对数函数泰勒展开：

以及广义二项式定理

常用的该机还是得记住的，另外还有一点是一定要关注收敛域 一定要关注收敛域 一定要关注收敛域

2.2 泰勒展开DLC

就两个。算不上重要。
引理：
设在区域内解析，且不是恒等于零的函数。若且，则存在的邻域，使得除外，内无其他满足的点。换句话说，的零点在内都是孤立的。
内部唯一性定理：
设与是在区域内解析的函数。
若存在一列点

满足

并且对所有，有

则

其实还有两个推论但是确实没啥意思也不重要

3. 洛朗级数展开

3.1 洛朗级数

3.1.1 洛朗级数定义

形如

是以为心的洛朗级数

3.1.2 收敛定理

洛朗级数的收敛域若存在，则必为环域，且和函数在环域内解析，在任意更窄的环域上一致收敛

3.2 洛朗展开定理

在以b为中心的环域内解析的函数必可展开为洛朗级数：

其中

并且展开唯一

实际在应用中我们并不会真的拿这个定理一点点算洛朗级数展开，而是拿已知结果推算。后面会给一道例题。

3.3 收敛范围

只是强调一下要注意范围实际上没啥东西。

例题：求

在附近环域和的洛朗级数展开
Tips: 第一种直接用几何级数，第二种上下同时除以z再变形然后用几何级数
是的我们其实就是尬蹭指数级数和几何级数

4. 奇点

其实这部分就是各种奇点的定义，也都是望文生义的东西。列举一下：
有限大孤立奇点（孤立的意思就是嘿！我们今天晚上有个超棒的派对，邻域里所有的解析点都会参加，猜猜谁没有被邀请？you！）、无穷远孤立奇点、孤立奇点、可去奇点、m级极点、本性奇点（无穷阶负幂次项）

再来道例题吧。求的所有有限大小奇点，并且在这些奇点的去心邻域做洛朗展开到前三阶非零项。
Tips: 判断极点阶数就是判断分母零点级数，判断分母零点级数只需要求导。
Tips: 不论在哪个地方展开，都最好先换元

第四章 留数定理

最有用的一集

1. 留数定理

1.1 留数定理

连续列三个“留数定理”感觉莫名好笑

留数定理 ：设是一个复变函数。若在简单闭正向曲线所围区域的内部除有限个孤立奇点外处处解析，且在曲线上也解析，则有：

其中是其洛朗级数展开式中项的系数，即：

其实这完全就是柯西积分定理

和之前的例题结论

的直接推论

1.2 留数的常用计算方式

简单极点

法则Ⅰ ：

或者，
法则Ⅱ ：如果且，则

阶极点

法则Ⅲ ：

本性奇点

没啥说的乖乖用柯西积分公式或者洛朗级数展开算吧😆

一般来说其实如果不是一阶极点感觉还不如直接洛朗展开

1.3 无穷远处的留数

无穷远处留数定义

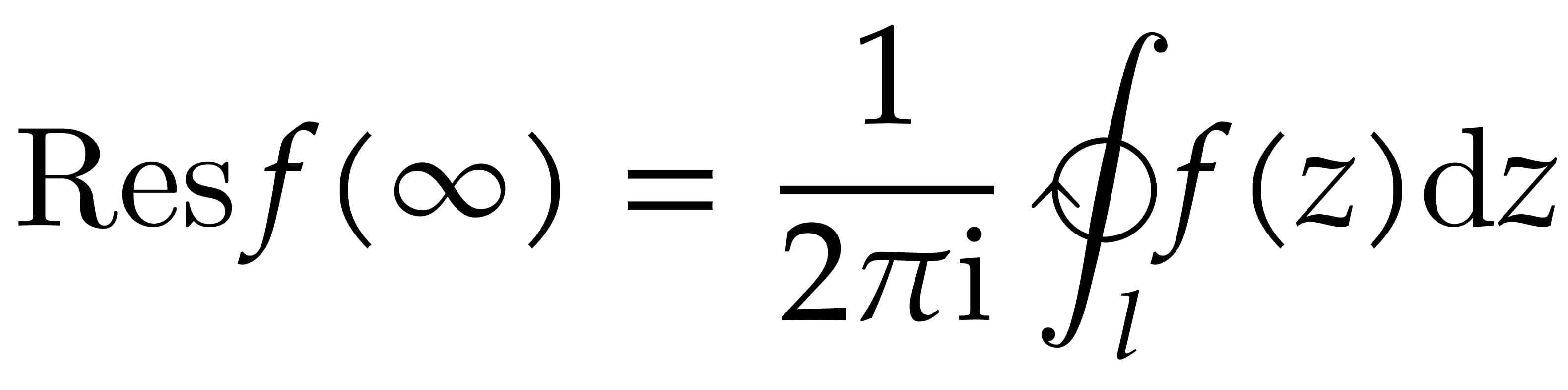
牛魔带方向的环路积分符号Latex居然还得额外加载包……实在懒得弄还是图片吧
这图片怎么这么大

无穷远留数的另一种计算方法

不知道具体用处先欠着（（（

2. 留数定理计算实积分

2.1 三个引理

2.1.1 大弧线引理

设在圆弧上连续且

在上一致成立，则：

顺带一提参数化是这种直接积分的最佳考量方式

2.1.2 约当引理

设当时函数在包括实轴的上半平面中一致趋于零，则当时：

其中

2.1.3 小弧引理

设在圆弧上连续且

在上一致成立，则：

2.2 留数定理求实积分

首先讲一下柯西主值 ：定义柯西主值就是极限存在时，反常积分的极限值。

2.2.1 实轴上无奇点的无穷限积分

定理 ：若函数在上半平面有有限个有限大小的孤立奇点，实轴上无奇点；在含实轴的上半平面当时，一致趋近于0，则

2.2.2 乘以正余弦的无穷限积分

定理 ：若函数在上半平面有有限个有限大小的孤立奇点，实轴上无奇点；在含实轴的上半平面当时，一致趋近于0，，定义则有

为偶函数时

以及

为奇函数时

2.2.3 实轴上一级极点的无穷限积分

定理 ：若函数在上半平面有有限个有限大小的孤立奇点，实轴上有一级极点；在含实轴的上半平面当时，一致趋近于0，则

2.2.4 实轴上一级极点的无穷限积分但是有震荡项

定理 ：若函数在上半平面有有限个有限大小的孤立奇点，实轴上有一级极点；在含实轴的上半平面当时，一致趋近于0，，定义则有

其实带有震荡项的最大区别就是可以衰减得更慢一些

2.2.5 三角函数有理式积分

定理 ：设是关于的有理函数，且积分存在。则该积分可以表示为：

其中是单位圆，且函数由以下转换得到：

然后，根据留数定理，积分的值为：

这里，是函数在其位于单位圆内部（即）的所有孤立奇点处的留数。

最爱滴习题时间😋
习题一：
习题二：
习题三：
习题四：

第五章……好吧其实已经结束了

不知道你怎么想的，反正我只感觉到了心累……
希望期中考能考得不错……
顺带一提上面给的留数定理的例题都属于是较难的那种，自己独立做不出来不用太伤心（（（（（（（